Las propiedades de la potenciación son las que permiten resolver por diferentes métodos una potencia. Estas son:
Potencia de exponente 0
Toda potencia de exponente 0 y base distinta de 0 es igual a 1.
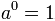 si se cumple que
si se cumple que 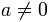
Potencia de exponente 1
Toda potencia de exponente 1 es igual a la base
Ejemplo:
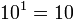
Potencia de exponente 0
Toda potencia de exponente 0 y base distinta de 0 es igual a 1.
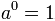 si se cumple que
si se cumple que 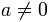
Potencia de exponente 1
Toda potencia de exponente 1 es igual a la base
Ejemplo:
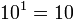
Producto de potencias de igual base
Para el producto de dos o más potencias de igual base se coloca la misma base y se suman los exponentes.
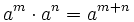
Ejemplo:
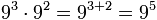
División de potencias de igual base
En la división de dos potencias de igual base se coloca la misma base y se restan los exponentes.
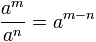
Potencia de un producto
La potencia de un producto de base (a·b) y de exponente "n" es igual a la potencia "a" a la "n" por "b" a la "n". Cada base se multiplica por el exponente.
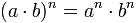
Potencia de una división
En la potencia de una división de base "a/b" y exponente "n" se procede a elevar cada uno de los componentes de la base a "n".
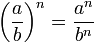
Potencia de una potencia
Para resolver la potencia de una potencia se coloca la misma base y se multiplican los exponentes.
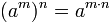
Propiedad distributiva
La potenciación es distributiva con respecto a la multiplicación y a la división, pero no lo es con respecto a la suma ni a la resta.
Distributiva con respecto a la multiplicación y división:
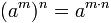
No es distributiva con respecto a la adición y sustracción:
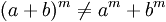
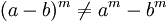
Propiedad conmutativa
La propiedad conmutativa no se cumple para la potenciación, exceptuando aquellos casos en que base y exponente tienen el mismo valor o son equivalentes.
En general:
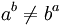
Propiedad asociativa
La propiedad asociativa no se cumple para la potenciación.
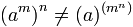
Potencia de base 10
Toda potencia de base 10 y que tiene como exponente un número natural es igual a la unidad seguida de la cantidad de ceros que indica el exponente.
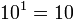
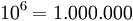
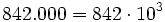
Potencia de exponente fraccionario
Es una potencia que tiene su exponente en forma de fracción, y en la que se cumple que

Potencia de exponente negativo
Una potencia que tenga exponente negativo se cambia de lugar y de este modo su exponente automáticamente cambiara a ser positivo
a − b = 1 / ab
Para el producto de dos o más potencias de igual base se coloca la misma base y se suman los exponentes.
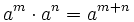
Ejemplo:
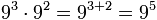
División de potencias de igual base
En la división de dos potencias de igual base se coloca la misma base y se restan los exponentes.
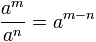
Potencia de un producto
La potencia de un producto de base (a·b) y de exponente "n" es igual a la potencia "a" a la "n" por "b" a la "n". Cada base se multiplica por el exponente.
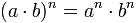
Potencia de una división
En la potencia de una división de base "a/b" y exponente "n" se procede a elevar cada uno de los componentes de la base a "n".
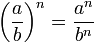
Potencia de una potencia
Para resolver la potencia de una potencia se coloca la misma base y se multiplican los exponentes.
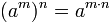
Propiedad distributiva
La potenciación es distributiva con respecto a la multiplicación y a la división, pero no lo es con respecto a la suma ni a la resta.
Distributiva con respecto a la multiplicación y división:
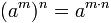
No es distributiva con respecto a la adición y sustracción:
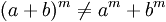
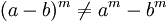
Propiedad conmutativa
La propiedad conmutativa no se cumple para la potenciación, exceptuando aquellos casos en que base y exponente tienen el mismo valor o son equivalentes.
En general:
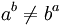
Propiedad asociativa
La propiedad asociativa no se cumple para la potenciación.
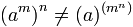
Potencia de base 10
Toda potencia de base 10 y que tiene como exponente un número natural es igual a la unidad seguida de la cantidad de ceros que indica el exponente.
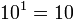
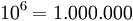
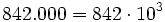
Potencia de exponente fraccionario
Es una potencia que tiene su exponente en forma de fracción, y en la que se cumple que

Potencia de exponente negativo
Una potencia que tenga exponente negativo se cambia de lugar y de este modo su exponente automáticamente cambiara a ser positivo
a − b = 1 / ab


