BLOG DE LA POTENCIACION
martes, 11 de marzo de 2014
domingo, 2 de marzo de 2014
BIENVENIDOS A MI BLOG MATEMATICO DE LA POTENCIACION
Espero les sea de mucha utilidad para ampliar sus conocimientos en este tema. ¡BUENA SUERTE!
EJERCICIOS DE POTENCIACION
| EJERCICIOS PARA PRACTICAR | |||
|---|---|---|---|
| 1 |  | ||
Aplicamos la definición de potencia, es decir, multiplicamos la base por sí misma tantas veces como indica el exponente. | |||
| 2 |  | ||
Puesto el exponente es negativo, primero expresamos la potencia como fracción. Nos queda el exponente en el denominador, así que aplicamos la definición de potencia al denominador.  | |||
| 3 |  | ||
Tenemos la potencia de una potencia. Aplicamos la regla, que consiste en multiplicar ambos exponentes y obtenemos una potencia con exponente negativo. Continuamos del mismo modo que en el ejercicio anterior.  | |||
| 4 |  | ||
Tenemos el cociente de dos potencias. Puesto que la base es la misma, la regla dice que se restan los exponentes (el del numerador menos el del denominador). Se obtiene un exponente negativo. | |||
| 5 |  | ||
Tenemos un producto de potencias en el numerador, pero no podemos efectuarlo al tener bases distintas (2 y 3). En el denominador tenemos una potencia de base 6 (3·2). Así, escribimos la potencia del denominador como un producto de potencias de bases 3 y 2, usando las reglas.  | |||
| 6 |  | ||
Primero podemos deshacernos del signo negativo del exponente de la primera potencia escribiendo la inversa de la fracción. Así, tendremos divisiones de potencias con las mismas bases. | |||
| 7 |  | ||
Aplicamos las reglas de las potencias a cada una de ellas para simplificar la expresión. Transformamos las bases en otras (aplicando potencias) para tener bases comunes.  | |||
| 8 |  | ||
El mayor problema en esta expresión es el gran número de bases distintas que tienen las potencias. Así que lo que haremos será usar las descomposición de cada base para solucionarlos. Notemos que 10=2·5 y 60=6·10=2·3·2·5. Después, sólo tenemos que multiplicar o dividir potencias.  | |||
| 9 |  | ||
Aplicamos las propiedades de las potencias, primero en los paréntesis que se irán simplificando.  | |||
| 10 |  | ||
Tenemos un exponente alto, pero no debemos preocuparnos por ello. Lo importante de este ejercicio es que la base de la potencia, que es todo el paréntesis, es una resta y no tenemos reglas para desarrollarla. Por tanto, tenemos que trabajar en el interior del paréntesis para poder aplicar las reglas.  | |||
| 11 |  | ||
El único problema de este ejercicio es la potencia de base 18, pero podemos escribir 18 como 18=3·6=3·2·3. Después, aplicamos las reglas.  | |||
| 12 |  | ||
Tenemos muchos exponentes. Aplicamos el la regla al primero, que es la potencia de un producto. Tenemos que identificar claramente los factores del producto para aplicar las reglas sin cometer errores. Luego continuamos con los otros exponentes.  | |||
| 13 |  | ||
Nos deshacemos del primer exponente, que es -1, lo que significa escribir la inversa de la base. También tenemos bases distintas, pero ya sabemos cómo solucionarlo: escribiendo las bases como productos y reagrupando las potencias. Recordemos que el símbolo " : " es una división, que es lo mismo que " / ".  | |||
| 14 |  | ||
El problema de este ejercicio son los parámetros, es decir, las letras. Se trabaja con ellas del mismo modo que con los número (los parámetros representan números). | |||
| 15 |  | ||
Lo más cómodo es escribir las divisiones ":" en forma de fracciones, "/". Una vez hecho, sólo queda aplicar las reglas.  | |||
| 16 |  | ||
La mayor dificultad es el gran número de parámetros. Aplicamos las reglas de las potencias para poder agrupar las potencias con la misma base alfabética.  | |||
| 17 |  | ||
 | |||
| 18 |  | ||
 | |||
| 19 |  | ||
 | |||
| 20 |  |
||
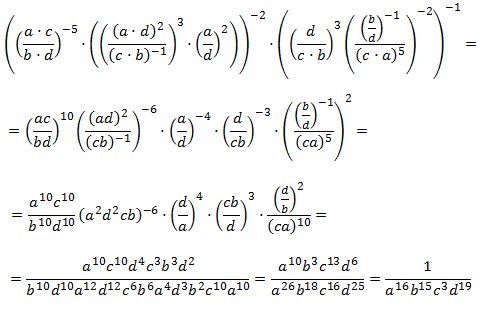 | |||
LA POTENCIACION Y SUS PROPIEDADES
Para un aprendizaje mas practico, te recomiendo que veas este video.
martes, 25 de febrero de 2014
PROPIEDADES DE LA POTENCIACION
Las propiedades de la potenciación son las que permiten resolver por diferentes métodos una potencia. Estas son:
Potencia de exponente 0
Toda potencia de exponente 0 y base distinta de 0 es igual a 1.
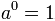 si se cumple que
si se cumple que 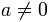
Potencia de exponente 1
Toda potencia de exponente 1 es igual a la base
Ejemplo:
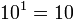
Potencia de exponente 0
Toda potencia de exponente 0 y base distinta de 0 es igual a 1.
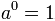 si se cumple que
si se cumple que 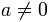
Potencia de exponente 1
Toda potencia de exponente 1 es igual a la base
Ejemplo:
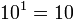
Producto de potencias de igual base
Para el producto de dos o más potencias de igual base se coloca la misma base y se suman los exponentes.
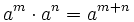
Ejemplo:
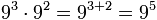
División de potencias de igual base
En la división de dos potencias de igual base se coloca la misma base y se restan los exponentes.
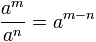
Potencia de un producto
La potencia de un producto de base (a·b) y de exponente "n" es igual a la potencia "a" a la "n" por "b" a la "n". Cada base se multiplica por el exponente.
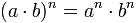
Potencia de una división
En la potencia de una división de base "a/b" y exponente "n" se procede a elevar cada uno de los componentes de la base a "n".
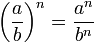
Potencia de una potencia
Para resolver la potencia de una potencia se coloca la misma base y se multiplican los exponentes.
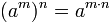
Propiedad distributiva
La potenciación es distributiva con respecto a la multiplicación y a la división, pero no lo es con respecto a la suma ni a la resta.
Distributiva con respecto a la multiplicación y división:
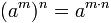
No es distributiva con respecto a la adición y sustracción:
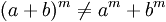
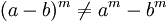
Propiedad conmutativa
La propiedad conmutativa no se cumple para la potenciación, exceptuando aquellos casos en que base y exponente tienen el mismo valor o son equivalentes.
En general:
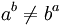
Propiedad asociativa
La propiedad asociativa no se cumple para la potenciación.
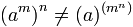
Potencia de base 10
Toda potencia de base 10 y que tiene como exponente un número natural es igual a la unidad seguida de la cantidad de ceros que indica el exponente.
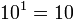
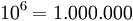
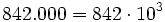
Potencia de exponente fraccionario
Es una potencia que tiene su exponente en forma de fracción, y en la que se cumple que

Potencia de exponente negativo
Una potencia que tenga exponente negativo se cambia de lugar y de este modo su exponente automáticamente cambiara a ser positivo
a − b = 1 / ab
Para el producto de dos o más potencias de igual base se coloca la misma base y se suman los exponentes.
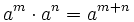
Ejemplo:
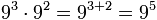
División de potencias de igual base
En la división de dos potencias de igual base se coloca la misma base y se restan los exponentes.
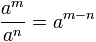
Potencia de un producto
La potencia de un producto de base (a·b) y de exponente "n" es igual a la potencia "a" a la "n" por "b" a la "n". Cada base se multiplica por el exponente.
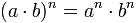
Potencia de una división
En la potencia de una división de base "a/b" y exponente "n" se procede a elevar cada uno de los componentes de la base a "n".
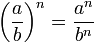
Potencia de una potencia
Para resolver la potencia de una potencia se coloca la misma base y se multiplican los exponentes.
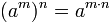
Propiedad distributiva
La potenciación es distributiva con respecto a la multiplicación y a la división, pero no lo es con respecto a la suma ni a la resta.
Distributiva con respecto a la multiplicación y división:
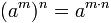
No es distributiva con respecto a la adición y sustracción:
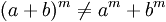
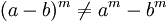
Propiedad conmutativa
La propiedad conmutativa no se cumple para la potenciación, exceptuando aquellos casos en que base y exponente tienen el mismo valor o son equivalentes.
En general:
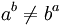
Propiedad asociativa
La propiedad asociativa no se cumple para la potenciación.
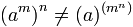
Potencia de base 10
Toda potencia de base 10 y que tiene como exponente un número natural es igual a la unidad seguida de la cantidad de ceros que indica el exponente.
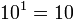
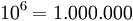
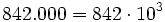
Potencia de exponente fraccionario
Es una potencia que tiene su exponente en forma de fracción, y en la que se cumple que

Potencia de exponente negativo
Una potencia que tenga exponente negativo se cambia de lugar y de este modo su exponente automáticamente cambiara a ser positivo
a − b = 1 / ab
Suscribirse a:
Entradas (Atom)